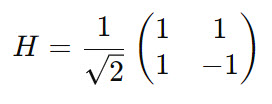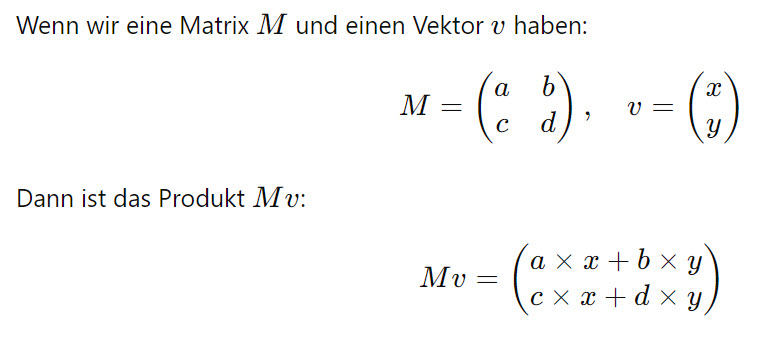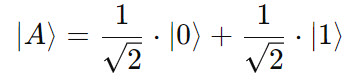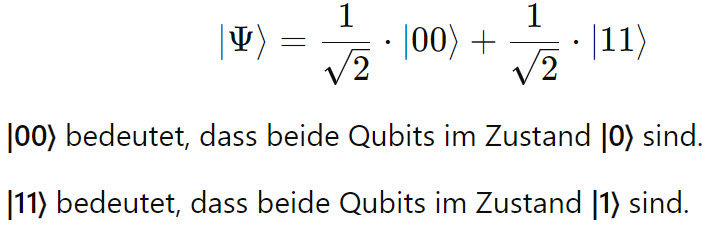Stand
27.10.2024 - Dr. Erhard Henkes
Quantencomputer - einfach erklärt
Einführung
Zum Verständnis klassischer Elektronik und
Computer benötigt man nicht unbedingt ein Verständnis der
Quantenphysik. Früher gab es die Elektronenröhren, später die
Transistoren.
In der Digitaltechnik verwendet man Transistoren
als elektronische Schalter. Man benötigt kein Verständnis, wie
ein Transitor physikalisch funktioniert, um die grundlegenden
"Gatter" wie NOT, AND, NAND, OR, NOR oder XOR und
hintereinander geschaltete Kombinationen hiervon zu verstehen. Man
verwendet die Ziffern 0 und 1 des Dualsystems
für Eingänge und Ausgänge. Ein AND hat zwei Eingänge. Setzt man
beide Eingänge auf 1, dann erhält man eine 1 am Ausgang. Alle
anderen Zustände führen zu 0 am Ausgang. Beschrieben wird all das
in der sogenannten Bitlogik,
die man sowohl bei Hardware als auch bei Software einsetzen kann.
Quantencomputer bieten hier eine interessante
Weiterentwicklung mittels Superposition
und Verschränkung,
die eine Parallelität und damit enorme Beschleunigung erlaubt. Wir
stehen noch ganz am Anfang dieser faszinierenden Entwicklung. Es ist
jedoch an der Zeit, dass man die grundlegenden Konzepte und Begriffe
versteht. Für die nachfolgenden Erläuterungen setze ich die
Künstliche Intelligenz ChatGPT ein, die es meisterhaft versteht, die
komplizierten Konzepte nicht nur auf Hochschulniveau, sondern auch
für Kinder und Jugendliche zu erklären, ohne hierbei gleich mit
linearer Algebra, Matrizen und imaginären Zahlen abzuschrecken.
Höhrere Mathematik ist für das grundlegende Verständnis nicht
notwendig, eher sogar hinderlich. Es soll also darum gehen, die
Vorteile und Funktion eines Quantencomputers zu verstehen, ohne ein
Mathematik- und Physikstudium absolvieren zu müssen. Es hilft
natürlich, wenn man das Dualsystem und die klassische Bitlogik
kennt, denn Quantencomputer benutzen diese digitale Technik genau wie
klassische elektronische Rechner.
Es hilft ebenso, wenn man physikalische
Konzepte wie Energie/Masse, Teilchen/Welle, Bohrsches
Atommodell/Orbitaltheorie kennt, da das Paar Bit/Quantenbit in diese
Reihe passt. Wir steigen nun in diese faszinierende neue Welt ein.
Quantenbit
Als Schreibweise findet man Qubit,
Qbit, Q-Bit usw. Empfohlen sei hier "Qubit".
Wie bereits erwähnt, nutzen klassische Computer mit Transistorlogik
das Bit als kleinste Informationseinheit, die entweder den Zustand 0
oder 1 annehmen kann (Spannung: z.B. ca. 0 oder 5 Volt). Diese Bits
werden in logischen Schaltungen verarbeitet, um Berechnungen
durchzuführen. Quantencomputer nutzen nun Qubits
(Quantum Bits), die sich aufgrund quantenmechanischer Eigenschaften
in einer Überlagerung (Superposition) befinden können, also
gleichzeitig(!) 0 und 1 sein können. Dies
ermöglicht eine parallele Verarbeitung von Informationen,
die bei klassischen Computern nicht möglich ist. Zusätzlich können
Qubits miteinander "verschränkt" werden, was bedeutet,
dass der Zustand eines Qubits direkt vom Zustand eines anderen
abhängt, unabhängig von der räumlichen Trennung. Diese
Verschränkung (Entanglement) ist wesentlich für die
Leistungsfähigkeit von Quantencomputern. Qubits können mittels
Quantenlogikgatter (Quantum Gates) verarbeitet werden, genau wie bei
klassischen Computern.
Hadamard-Gatter
Wir fangen mit dem einfachsten Gatter an,
nämlich dem Hadamard-Gatter, und erklären es einfach.
Stell
dir vor, ein Quantencomputer arbeitet mit Qubits,
die sich wie kleine Lichtschalter verhalten, die nicht nur ein- oder
ausgeschaltet sein können, sondern auch irgendwo dazwischen.
Ein
Hadamard-Gatter ist nun eine spezielle Art von
Schalter, der einem Qubit hilft, diese „Zwischenzustände“, also
gleichzeitig 0 und 1, zu erreichen.
Einfaches Beispiel mit Münzen
Um das Hadamard-Gatter zu verstehen, benutzen
wir ein einfaches Beispiel mit einer Münze:
Klassische Münze (klassisches
Bit):
Quanten-Münze (Qubit):
Was macht das Hadamard-Gatter?
Das Hadamard-Gatter ist wie ein besonderer
Trick, den du mit der Quanten-Münze machst:
Warum ist das wichtig?
Dieser Zwischenzustand ist wichtig für
Quantencomputer, weil er es ermöglicht, viele Berechnungen
gleichzeitig durchzuführen. Stell dir vor, du könntest viele
Aufgaben auf einmal erledigen, anstatt sie nacheinander zu machen –
das ist ungefähr das, was Quantencomputer mit Hilfe von
Hadamard-Gattern tun können.
Anschauliche Vorstellung
Denke an das Hadamard-Gatter wie an eine
spezielle Drehbewegung deiner Quanten-Münze:
Startzustand:
Drehung mit dem Hadamard-Gatter:
Nach der Drehung:
Zusammenfassung
Hadamard-Gatter ist ein
spezieller „Schalter“ für Qubits in einem Quantencomputer.
Es verwandelt ein Qubit von einem klaren
Zustand (entweder 0 oder 1) in einen Zwischenzustand (eine Mischung
aus 0 und 1).
Dadurch können Quantencomputer viele
Dinge gleichzeitig berechnen und sind so viel schneller bei
bestimmten Aufgaben als klassische Computer.
CNOT-Gatter
Stell dir vor, du hast zwei Quanten-Münzen
statt nur einer. Diese beiden Münzen arbeiten zusammen, und das
CNOT-Gatter ist eine spezielle Art von „Zaubertrick“.
Dieser
steuert, wie die eine Münze die andere beeinflusst.
Zwei Münzen, zwei Aufgaben
Die Kontroll-Münze (Control
Qubit):
Diese Münze
bestimmt, ob der Trick ausgeführt wird oder nicht. Sie ist wie der
Anführer, der entscheidet, was passiert.
Die Ziel-Münze (Target Qubit):
Wie funktioniert das CNOT-Gatter?
Stell dir vor, du hast zwei Münzen:
Das CNOT-Gatter funktioniert nach folgender
Regel:
Anschauliches Beispiel
1. Ausgangssituation:
Münze A:
Kopf (0)
Münze B:
Kopf (0)
Anwendung des CNOT-Gatters:
Ergebnis:
Münze A:
Kopf (0)
Münze B:
Kopf (0)
2. Ausgangssituation:
Münze A:
Zahl (1)
Münze B:
Kopf (0)
Anwendung des CNOT-Gatters:
Ergebnis:
Münze A:
Zahl (1)
Münze B:
Zahl (1)
3. Ausgangssituation:
Münze A:
Zahl (1)
Münze B:
Zahl (1)
Anwendung des CNOT-Gatters:
Ergebnis:
Münze A:
Zahl (1)
Münze B:
Kopf (0)
4. Ausgangssituation:
Münze A:
Kopf (0)
Münze B:
Zahl (1)
Anwendung des CNOT-Gatters:
Ergebnis:
Münze A:
Kopf (0)
Münze B:
Zahl (1)
Warum ist das wichtig?
Das CNOT-Gatter ist wichtig, weil es
Verschränkung (Entanglement) zwischen den beiden
Quanten-Münzen herstellen kann. Das bedeutet, dass die beiden Münzen
miteinander verbunden sind, sodass der Zustand der einen Münze den
Zustand der anderen beeinflusst, selbst wenn sie weit voneinander
entfernt sind. Diese Eigenschaft ist einer der Grundsteine für die
unglaubliche Rechenleistung von Quantencomputern.
Zusammenfassung
CNOT-Gatter
arbeitet mit zwei
Qubits:
einer Kontroll-Münze und einer Ziel-Münze.
Regel:
Wenn die Kontroll-Münze
Zahl (1)
zeigt, dreht das Gatter
die Ziel-Münze. Zeigt sie Kopf
(0),
bleibt die Ziel-Münze unverändert.
Bedeutung:
Es hilft dabei,
Quanten-Münzen zu verknüpfen (Verschränkung), was
Quantencomputern ihre besondere Kraft verleiht.
Einfaches Bild zur Vorstellung
Stell dir vor, du hast zwei Lichtschalter im
Raum:
Schalter A (Kontroll):
Bestimmt, wie Schalter B funktioniert.
Schalter B (Ziel):
Schaltet das Licht ein oder aus.
Wenn Schalter A aus ist (Kopf):
Schalter B funktioniert normal. Du kannst das Licht an- oder
ausschalten.
Wenn Schalter A an ist (Zahl):
Jedes Mal, wenn du versuchst, Schalter B zu betätigen, passiert das
Gegenteil des Erwarteten. Versuchst du das Licht einzuschalten,
bleibt es aus, und umgekehrt.
Das CNOT-Gatter steuert also, wie der eine
Schalter den anderen beeinflusst, basierend darauf, ob der erste
Schalter an oder aus ist.
CNOT steht für Controlled
NOT Gate.
Toffoli-Gatter
Stell dir vor, du hast drei
Quanten-Münzen (Qubits), die zusammenarbeiten. Das
Toffoli-Gatter ist ein spezieller „Zaubertrick“,
der alle drei Münzen gleichzeitig beeinflusst. Es ist wie ein sehr
intelligenter Schalter, der nur dann eine Aktion ausführt, wenn
bestimmte Bedingungen erfüllt sind.
Drei Münzen, eine Regel
Zwei
Kontroll-Münzen (Control Qubits):
Eine
Ziel-Münze (Target Qubit):
Wie funktioniert das Toffoli-Gatter?
Stell dir vor, du hast drei Münzen:
Münze
A (erste Kontroll-Münze): Kann
Kopf (1) oder Zahl (0) zeigen.
Münze
B (zweite Kontroll-Münze): Kann
ebenfalls Kopf (1) oder Zahl (0) zeigen.
Münze C
(Ziel-Münze): Startet
auf Zahl (0) oder Kopf (1).
Das Toffoli-Gatter folgt dieser einfachen
Regel:
Anschauliches Beispiel mit Münzen
Beispiel 1: Beide Kontroll-Münzen
sind Kopf
Beispiel 2: Eine Kontroll-Münze ist
Kopf, die andere Zahl
Beispiel 3: Beide Kontroll-Münzen
sind Zahl
Warum ist das wichtig?
Das Toffoli-Gatter ist besonders nützlich,
weil es logische Bedingungen in einem
Quantencomputer überprüfen kann.
Es ermöglicht komplexere
Operationen, bei denen mehrere Bedingungen gleichzeitig betrachtet
werden. Dadurch können Quantencomputer noch leistungsfähiger und
vielseitiger werden.
Ein weiteres anschauliches Bild
Stell dir vor, du hast drei Lichtschalter in
deinem Zimmer:
Schalter A und B: Diese
bestimmen, ob ein spezielles Licht eingeschaltet wird.
Schalter C: Das Licht
selbst.
Regel:
Wenn
beide Schalter A und B eingeschaltet sind: Schalter
C schaltet das Licht verdreht. Wenn es aus ist, geht es an; wenn es
an ist, geht es aus.
Andernfalls:
Schalter C bleibt
unverändert und das Licht bleibt so, wie es ist.
Zusammenfassung
Toffoli-Gatter:
Ein spezielles
Quanten-Gatter, das mit drei
Qubits arbeitet.
Regel:
Es dreht die dritte Münze
(Ziel-Münze) nur dann, wenn die ersten beiden Münzen
(Kontroll-Münzen) beide Kopf zeigen.
Bedeutung:
Es erlaubt
Quantencomputern, komplexe Bedingungen zu prüfen und dadurch
leistungsfähigere Berechnungen durchzuführen.
Warum ist das cool?
Durch die Kombination von Hadamard-, CNOT- und
Toffoli-Gattern können Quantencomputer bereits sehr komplexe
Aufgaben lösen, die für klassische Computer schwierig bis unmöglich
sind. Das macht sie zu mächtigen technologischen Werkzeugen der
Zukunft.
Volladdierer nach Feynman
Was ist ein Volladdierer?
Bevor wir zum quantum
Volladdierer kommen, lass uns zuerst verstehen, was ein klassischer
Volladdierer ist.
Klassischer Volladdierer:
Stell dir vor, du möchtest zwei Zahlen im
Binärsystem (also nur mit 0 und 1) addieren. Ein Volladdierer
ist eine kleine Schaltung, die drei Eingaben verarbeitet:
A:
Die erste Binärziffer
(z.B. 0 oder 1)
B:
Die zweite Binärziffer
(z.B. 0 oder 1)
C_in:
Der Übertrag von der
vorherigen Stelle (z.B. 0 oder 1)
Der Volladdierer gibt zwei Ausgaben:
Summe
(S): Das
Ergebnis der Addition dieser drei Eingaben (ebenfalls 0 oder 1)
Übertrag
(C_out): Der
Übertrag, der zur nächsten Stelle weitergegeben wird (ebenfalls 0
oder 1)
Beispiel:
Eingaben:
A = 1, B = 1, C_in = 0
Summe
(S): 0
(weil 1 + 1 + 0 = 10 in Binär, also 0 mit einem Übertrag von 1)
Übertrag
(C_out): 1
Quanten-Volladdierer nach Feynman:
Ein quantum Volladdierer
funktioniert ähnlich, aber er nutzt die besonderen Eigenschaften von
Qubits und Quanten-Gattern, um die
Addition durchzuführen. Hier ist eine vereinfachte Erklärung:
1. Die Bausteine: Qubits und
Quanten-Gatter
Qubits:
Wie zuvor besprochen,
können sie 0 und 1 gleichzeitig sein (Superposition).
Quanten-Gatter:
Spezielle „Schalter“,
die die Qubits manipulieren, ähnlich wie logische Gatter in
klassischen Computern.
2. Aufbau des Quanten-Volladdierers:
Der Quanten-Volladdierer benötigt mehrere
Qubits und Quanten-Gatter, um die drei Eingaben (A, B, C_in) zu
verarbeiten und die zwei Ausgaben (Summe, C_out) zu erzeugen.
Schritte:
Eingabe-Qubits vorbereiten:
Verwenden von CNOT- und
Toffoli-Gattern:
CNOT-Gatter:
Wie zuvor erklärt,
beeinflusst ein Qubit ein anderes basierend auf seinem Zustand.
Summe berechnen:
Übertrag berechnen:
Das Toffoli-Gatter
wird verwendet, um den Übertrag C_out zu berechnen, basierend
darauf, ob mindestens zwei der Eingaben 1 sind.
Anschauliches Beispiel mit Münzen:
Stell dir vor, du hast drei Quanten-Münzen:
Münze
A: Repräsentiert
den ersten Binärwert (A)
Münze
B: Repräsentiert
den zweiten Binärwert (B)
Münze
C_in: Repräsentiert
den Übertrag von der vorherigen Addition
Und zwei Ausgabe-Münzen:
Wie funktioniert das?
Eingabe:
Quanten-Gatter anwenden:
CNOT-Gatter:
Wenn Münze A Kopf ist,
beeinflusst sie Münze S.
Toffoli-Gatter:
Wenn sowohl Münze A als
auch Münze B Kopf sind, beeinflusst sie Münze C_out.
Ergebnis:
Beispiel:
Das entspricht dem klassischen Beispiel, wo 1
+ 1 + 0 = 10 (Summe 0 mit Übertrag 1).
Warum ist das wichtig?
Der Quanten-Volladdierer ist ein Baustein für
komplexere Quantenrechner. Er zeigt, wie man grundlegende
arithmetische Operationen mit Quanten-Gattern durchführen kann.
Durch die Nutzung von Superposition und Verschränkung können
Quantencomputer viele Berechnungen gleichzeitig ausführen, was sie
bei bestimmten Aufgaben viel
schneller macht als klassische Computer.
Zusammenfassung:
Volladdierer:
Ein Gerät, das drei
Binärziffern (A, B, C_in) addiert und eine Summe (S) sowie einen
Übertrag (C_out) liefert.
Quanten-Volladdierer
nach Feynman: Nutzt
Qubits und Quanten-Gatter wie CNOT und Toffoli, um die Addition auf
der Quantenebene durchzuführen.
Anschauliches
Bild: Denk
an Quanten-Münzen, die durch spezielle „Zaubertricks“
(Quanten-Gatter) manipuliert werden, um die Summe und den Übertrag
zu berechnen.
Wichtigkeit:
Ermöglicht komplexe
Berechnungen in Quantencomputern, die bei klassischen Computern zu
lange dauern würden.
Einfacher Quantenalgorithmus mit
Quantenvolladdierer
Wir werden einen Quanten-Volladdierer
verwenden, um zwei Binärzahlen zu addieren. Stell dir vor, du hast
zwei einfache Zahlen (jeweils 0 oder 1) und möchtest sie
zusammenzählen. Unser Quantenalgorithmus wird dies auf eine
besondere Weise tun, indem er die Macht der Quanten nutzt.
Die Bausteine, die wir brauchen:
Drei Quanten-Münzen (Qubits):
Qubit
A: Die
erste Zahl (0 oder 1)
Qubit
B: Die
zweite Zahl (0 oder 1)
Qubit
C_in: Der
Übertrag von einer vorherigen Addition (für den Anfang setzen wir
ihn auf 0)
Zwei weitere Quanten-Münzen für
die Ausgaben:
Quanten-Gatter:
CNOT-Gatter:
Beeinflusst ein Qubit
basierend auf einem anderen
Toffoli-Gatter:
Ein spezielles Gatter,
das drei Qubits gleichzeitig beeinflusst
Schritt-für-Schritt-Anleitung des
Algorithmus:
1. Vorbereitung der Eingaben:
Stell dir vor, wir wollen die Zahlen A
= 1 und B = 1 addieren, und der anfängliche
Übertrag C_in = 0 ist.
2. Anwendung der CNOT-Gatter zur
Berechnung der Summe (S):
Das Ziel ist es, die Summe S
zu berechnen, ohne den Übertrag zu berücksichtigen.
Erstes
CNOT-Gatter: Kontrolliert
durch A,
beeinflusst S
Zweites
CNOT-Gatter: Kontrolliert
durch B,
beeinflusst S
Zwischenergebnis:
3. Anwendung des Toffoli-Gatters zur
Berechnung des Übertrags (C_out):
Der Übertrag C_out entsteht,
wenn mindestens zwei der Eingaben A, B
oder C_in gleich 1 sind.
Zwischenergebnis:
4. Ergebnis der Addition:
Nach der Anwendung der Gatter haben wir:
Summe
(S): 0
Übertrag
(C_out): 1
Das entspricht der binären Addition von 1
+ 1 = 10 (Summe 0 mit einem Übertrag von 1).
Ein weiteres Beispiel:
Lass uns ein anderes Beispiel durchgehen, um
es noch klarer zu machen.
Beispiel: A = 1, B = 0, C_in = 1
Eingaben:
Schritte:
CNOT-Gatter mit A auf S:
CNOT-Gatter mit B auf S:
Toffoli-Gatter mit A und B auf
C_out:
Ergebnis:
Summe
(S): 1
Übertrag
(C_out): 0
Das entspricht der binären Addition von 1
+ 0 + 1 = 10 (Summe 0 mit einem Übertrag von 1). Allerdings
sehen wir hier, dass C_out eigentlich 1 sein sollte,
was bedeutet, dass in unserem einfachen Beispiel der Toffoli-Gatter
nur dann den Übertrag beeinflusst, wenn beide A und
B 1 sind. Um auch den C_in zu
berücksichtigen, müsste der Volladdierer erweitert werden. Aber für
den Anfang reicht dieses Beispiel, um die Grundidee zu verstehen.
Warum ist das wichtig?
Dieser einfache Quanten-Algorithmus zeigt, wie
Quantencomputer grundlegende Rechenoperationen durchführen können,
ähnlich wie klassische Computer, aber mit den besonderen
Eigenschaften der Quantenphysik. Superposition und
Verschränkung erlauben es Quantencomputern,
komplexe Berechnungen schneller und damit effizienter durchführen.
Zusammenfassung:
Quanten-Volladdierer:
Ein Quantenalgorithmus,
der zwei Binärzahlen und einen Übertrag addiert.
Benutzte
Gatter: CNOT-Gatter
zur Berechnung der Summe und Toffoli-Gatter zur Berechnung des
Übertrags.
Eingaben
und Ausgaben: Wir
geben zwei Zahlen und einen Übertrag ein und erhalten eine Summe
und einen neuen Übertrag.
Anschauliche
Vorstellung: Denk
an Quanten-Münzen, die durch spezielle „Zaubertricks“
(Quanten-Gatter) manipuliert werden, um die Addition durchzuführen.
Dieser einfache Algorithmus ist ein
Grundbaustein für komplexere Quantenrechnungen und zeigt, wie
Quantencomputer mit den speziellen Eigenschaften der Quantenmechanik
arbeiten, um Informationen zu verarbeiten.
Beschleunigung durch Quantencomputer
Warum sind Quantencomputer schneller?
Superposition:
Klassische
Bits können
entweder 0 oder 1 sein.
Qubits
können gleichzeitig
0 und 1 sein,
also in mehreren Zuständen gleichzeitig existieren.
Das
bedeutet, dass ein Quantencomputer viele
mögliche Lösungen gleichzeitig ausprobieren kann.
Verschränkung:
Qubits
können miteinander verbunden sein, sodass der Zustand eines Qubits
direkt den Zustand eines anderen beeinflusst, egal wie weit sie
voneinander entfernt sind.
Diese
Verbindungen ermöglichen es, komplexe Probleme effizienter zu
lösen, weil Informationen schneller und verknüpfter verarbeitet
werden.
Quantenparallelität:
Durch
Superposition und Verschränkung können Quantencomputer viele
Berechnungen gleichzeitig durchführen.
Das ist, als ob du
nicht nur einen Weg überprüfst, sondern dir alle möglichen Wege
gleichzeitig
anschaust.
Einfaches Beispiel:
Stell dir vor, du untersuchst eine bestimmte
Kombination von zwei Münzen (z.B. Kopf-Kopf, Kopf-Zahl, Zahl-Kopf,
Zahl-Zahl). Ein klassischer Computer muss jede Kombination einzeln
überprüfen. Ein Quantencomputer kann dank der Superposition alle
Kombinationen gleichzeitig betrachten und so viel schneller die
richtige finden.
Zusammenfassung:
Die Beschleunigung von
Quantencomputern kommt also dadurch zustande, dass durch
Superposition und Verschränkung
viele Möglichkeiten gleichzeitig verarbeitet
werden.
Das macht Quantencomputer bei bestimmten Aufgaben, wie
komplexen Berechnungen oder der Suche in großen Datenmengen,
deutlich schneller als klassische Computer.
Konkretes Beispiel: Faktorisieren
Wir schauen nun ein konkretes Beispiel
an, bei dem Quantencomputer gegenüber klassischen
Computern einen riesigen Vorteil haben.
Ein bekanntes
Beispiel ist das Faktorisieren großer Zahlen.
Dafür nutzen wir den Shor-Algorithmus.
Faktorisieren bedeutet, eine große Zahl in
ihre kleinsten Bausteine (Faktoren) zu zerlegen, die miteinander
multipliziert die ursprüngliche Zahl ergeben.
Beispiel:
Warum ist das Faktorisieren wichtig?
Das Faktorisieren großer Zahlen ist besonders
wichtig für die Kryptographie, also die Sicherheit
von Informationen im Internet. Viele Verschlüsselungssysteme, wie
RSA, basieren darauf, dass das Faktorisieren sehr
großer Zahlen (mit hunderten oder tausenden von Stellen) extrem
schwierig und zeitaufwändig ist - zumindest für klassische
Computer.
Klassische Computer vs.
Quantencomputer
Klassische Computer:
Arbeitsweise:
Klassische Computer
probieren systematisch nacheinander verschiedene Faktoren aus, bis
sie die richtigen finden.
Problem bei
großen Zahlen: Wird
die Zahl sehr groß (z.B. mit 300 Stellen), dauert das Ausprobieren
aller möglichen Faktoren sehr,
sehr lange – sogar
Millionen
von Jahren könnten
dafür nötig sein!
Quantencomputer:
Shor-Algorithmus:
Ein spezieller
Quantenalgorithmus, entwickelt von Peter Shor, der große Zahlen
viel schneller faktorisieren kann als jeder bekannte klassische
Algorithmus.
Geschwindigkeit:
Während ein klassischer
Computer Millionen von Jahren brauchen würde, um eine sehr große
Zahl zu faktorisieren, könnte ein Quantencomputer dies in
Stunden oder Tagen erledigen.
Konkretes Beispiel:
Stell dir vor, du hast eine Zahl wie
1.234.567.890.123.456.789 und möchtest sie
faktorisieren.
Warum ist das so bedeutend?
Sicherheit im Internet:
RSA-Verschlüsselung:
Wird weltweit zur
sicheren Kommunikation genutzt. Wenn ein Quantencomputer den
Shor-Algorithmus ausführen kann, könnte er die Verschlüsselung
knacken, indem er die großen Zahlen faktorisieren kann, auf denen
die Sicherheit basiert.
Folge:
Es würde notwendig sein,
neue Verschlüsselungsmethoden zu entwickeln, die auch für
Quantencomputer sicher sind.
Neue Möglichkeiten:
Fortschritte
in Wissenschaft und Technik: Schnellere
Faktorisierung könnte auch andere Bereiche wie
Materialwissenschaften, Chemie und mehr revolutionieren, da sie oft
komplexe Berechnungen und Simulationen erfordern.
Aktueller Stand:
Klassische
Computer: Sehr
gut darin, alltägliche Aufgaben zu bewältigen, aber bei extrem
großen Zahlen stoßen sie an ihre Grenzen.
Quantencomputer:
Noch in der Entwicklung,
aber bereits zeigen sie das Potenzial, bestimmte Probleme wie die
Faktorisierung viel schneller zu lösen. Unternehmen und
Forschungseinrichtungen arbeiten intensiv daran, leistungsfähigere
Quantencomputer zu bauen.
Zusammenfassung:
Problem:
Faktorisieren großer
Zahlen ist für klassische Computer extrem zeitaufwändig.
Lösung:
Quantencomputer nutzen den
Shor-Algorithmus, um dieses Problem deutlich schneller zu lösen.
Bedeutung:
Dies könnte die
Sicherheit im Internet beeinflussen und neue Möglichkeiten in
Wissenschaft und Technik eröffnen.
Warum ist das spannend?
Dieses Beispiel zeigt, wie Quantencomputer
grundlegende Probleme lösen können, die für
klassische Computer praktisch unlösbar sind. Es
verdeutlicht auch, wie revolutionär die Quantencomputing-Technologie
sein kann und warum sie so viel Aufmerksamkeit in der Forschung und
Industrie erhält. Dieses konkrete Beispiel zeigt, wie
Quantencomputer klassischen Computern überlegen sein können, indem
sie Probleme lösen, die für letztere unmöglich oder extrem
zeitaufwändig sind! Mehr Informationen findet man hier.
Technische
Möglichkeiten für einen Quantencomputer
Es gibt verschiedene Ansätze, wie man Qubits
– die Grundbausteine von Quantencomputern – realisieren kann.
Jeder Ansatz hat Stärken und Herausforderungen. Nachfolgend
sind die wichtigsten Technologien im Überblick aufgeführt:
1. Supraleitende Qubits
Wie funktionieren sie?
Materialien:
Nutzen supraleitende Materialien, die bei extrem niedrigen
Temperaturen keinen elektrischen Widerstand haben.
Schaltkreise:
Bestehen aus Schaltkreisen, die aus diesen supraleitenden
Materialien gefertigt sind und mikroskopisch kleine Schleifen
bilden.
Schwingungen:
Verwenden elektrische Schwingungen, um die Zustände der Qubits (0
und 1) darzustellen.
Vorteile:
Herausforderungen:
Kühlung:
Müssen auf Temperaturen nahe dem absoluten Nullpunkt (0 Kelvin oder
-273,15 °C) gekühlt werden, was aufwändig und kostspielig ist.
Dekohärenz:
Sehr anfällig für Störungen durch Umgebungsgeräusche und
Temperaturänderungen.
2. Ionenfallen
Wie funktionieren sie?
Ionen:
Verwenden geladene Atome (Ionen), die in elektromagnetischen Feldern
festgehalten werden.
Laser:
Nutzen Laserstrahlen, um die Zustände der Ionen zu manipulieren und
Qubits zu erzeugen.
Vorteile:
Hohe
Präzision:
Sehr genau und mit geringer Fehleranfälligkeit.
Langfristige
Kohärenz:
Ionen können ihre Zustände länger behalten, bevor sie gestört
werden.
Herausforderungen:
Skalierung:
Schwieriger zu skalieren auf viele Qubits im Vergleich zu
supraleitenden Qubits.
Komplexe
Steuerung:
Erfordert präzise Lasersteuerungen, was technisch anspruchsvoll
ist.
3. Photonische Qubits
Wie funktionieren sie?
Photonen:
Nutzen Lichtteilchen (Photonen) zur Darstellung von Qubits, z.B.
durch ihre Polarisation (Richtung der Schwingung).
Fasern:
Übertragen Informationen durch Glasfaserkabel, ähnlich wie in der
Telekommunikation.
Vorteile:
Herausforderungen:
Interaktion:
Es ist schwierig, starke Wechselwirkungen zwischen Photonen zu
erzeugen, die für Quantenlogikgatter nötig sind.
Technologie:
Die Technologie zur Manipulation und Messung von Photonen ist
komplex und noch in der Entwicklung.
4. Topologische Qubits
Wie funktionieren sie?
Topologische
Teilchen:
Nutzen spezielle Teilchen, die sogenannte Anyonen
sind und besondere topologische Eigenschaften haben.
Verschränkung:
Diese Teilchen sind weniger anfällig für Störungen und
Dekohärenz, da ihre Zustände durch ihre topologische Anordnung
geschützt sind.
Vorteile:
Fehlerresistenz:
Sehr stabil gegen Umgebungsstörungen, was die Fehlerkorrektur
erleichtert.
Langfristige
Speicherung:
Informationen können länger stabil gespeichert werden.
Herausforderungen:
5. Spins in Halbleitern
Wie funktionieren sie?
Vorteile:
Herausforderungen:
Dekohärenz:
Spins sind anfällig für Störungen durch Umgebungsfelder und
Materialfehler.
Kühlung:
Oft müssen auch diese Systeme sehr kalt gehalten werden, um stabil
zu funktionieren.
Zukunftsaussichten
Hybridansätze:
Kombination verschiedener Technologien, um die Stärken jeder
Methode zu nutzen und ihre Schwächen zu überwinden.
Fehlerkorrektur:
Weiterentwicklungen in der Quantenfehlerkorrektur sind entscheidend,
um stabile und skalierbare Quantencomputer zu bauen.
Materialforschung:
Neue Materialien und innovative Designs könnten die Leistung und
Skalierbarkeit von Qubits erheblich verbessern.
Zusammenfassung
Supraleitende
Qubits
sind derzeit weit verbreitet und gut skalierbar, aber benötigen
extrem niedrige Temperaturen.
Ionenfallen
bieten hohe Präzision und lange Kohärenzzeiten, sind aber schwerer
zu skalieren.
Photonische
Qubits
sind robust und ideal für Kommunikation, haben aber
Herausforderungen bei der Interaktion.
Topologische
Qubits
versprechen hohe Fehlerresistenz, sind aber noch in der Entwicklung.
Spins in
Halbleitern
bieten gute Integration mit bestehender Technologie, haben aber
ebenfalls Dekohärenzprobleme.
Jede dieser Technologien hat das Potenzial,
die Zukunft der Quantencomputer zu gestalten. Die Forschung ist aktiv
und es werden ständig neue Durchbrüche erzielt, die uns näher an
leistungsfähige und praktische Quantencomputer bringen.
Konkrete Beispiele für Quantencomputer
Wo werden aktuell die größten
Quantencomputer betrieben? Der Bereich des Quantencomputings
entwickelt sich rasant, und mehrere Unternehmen sowie
Forschungseinrichtungen sind führend in Entwicklung und Betrieb
leistungsstarker Quantencomputer.
Derzeit werden die größten und
leistungsfähigsten Quantencomputer durch führende
Technologieunternehmen (wie IBM, Google, Microsoft,
Quantinuum und IonQ), staatlich geförderte
Forschungsinitiativen (insbesondere in China) und
spezialisierte Firmen (wie D-Wave und Rigetti) betrieben.
1. IBM Quantum
Standorte:
Armonk,
New York (USA):
Hauptsitz von IBM Quantum.
Weitere
Zentren weltweit:
IBM betreibt Quantenzentren in Städten wie Zürich (Schweiz),
Tokio (Japan), und São Paulo (Brasilien).
Quantencomputer:
IBM
Quantum System One:
Eines der fortschrittlichsten Quantencomputersysteme, das in
verschiedenen IBM Quantum Zentren weltweit eingesetzt wird.
Qubit-Zahlen:
IBM arbeitet kontinuierlich an der Skalierung seiner Systeme und
hat bereits Quantencomputer mit über 100 Qubits angekündigt, mit
Plänen für noch größere Systeme.
2. Google Quantum AI
Standort:
Quantencomputer:
Sycamore-Prozessor:
Behauptung der "Quantenüberlegenheit"
im Jahr 2019,
bei der Sycamore eine spezifische Aufgabe schneller löste als der
leistungsstärkste klassische Supercomputer.
Weiterentwicklung:
Google arbeitet an weiter skalierbaren Prozessoren mit mehr Qubits
und verbesserter Fehlerkorrektur.
3. Microsoft Quantum
Standort:
Redmond,
Washington (USA):
Hauptsitz von Microsoft Quantum.
Forschungszentren:
Microsoft betreibt auch Quantenforschungszentren in Städten wie
Santa Barbara und anderen weltweit.
Quantencomputer:
Topologische
Qubits:
Microsoft investiert stark in die Entwicklung von topologischen
Qubits, die besonders stabil und fehlerresistent sein sollen.
Quantenentwicklungsplattform:
Microsoft bietet die Azure Quantum Plattform an, die Zugang zu
verschiedenen Quantencomputern und -ressourcen bietet.
4. Honeywell (nun Teil von
Quantinuum)
Standort:
Quantencomputer:
H1-System:
Eines der leistungsstärksten Quantencomputersysteme von Quantinuum
mit über 20 Qubits und hoher Fehlerkorrektur.
Skalierung:
Quantinuum plant die Erweiterung seiner Systeme mit mehr Qubits und
verbesserter Stabilität.
Standort:
College
Park, Maryland (USA):
Hauptsitz von IonQ.
Weitere
Standorte:
IonQ hat auch Forschungsstandorte in Dallas (Texas) und anderen
Städten.
Quantencomputer:
IonQ
Quantum Computers:
Nutzen Ionenfallen-Technologie mit hoher Genauigkeit und geringer
Fehleranfälligkeit.
Qubit-Zahlen:
IonQ arbeitet an Systemen mit über 100 Qubits und bietet Zugang zu
ihren Quantencomputern über Cloud-Plattformen an.
6. China – Nationale
Quantencomputing-Initiativen
Standorte:
Quantencomputer:
Jiuzhang-Photonen-Computer:
Entwickelt von Wissenschaftlern der Universität der Wissenschaften
in Peking, bekannt für ihre Leistung bei speziellen
Quantenaufgaben.
Andere
Entwicklungen:
China investiert massiv in Quantenkommunikation und
Quantencomputing, mit Projekten wie dem
Quantenkommunikationssatelliten „Micius“.
7. Andere führende Einrichtungen und
Unternehmen
D-Wave Systems (Kanada):
Standort:
Burnaby, British Columbia (Kanada).
Quantencomputer:
Spezialisieren sich auf Quanten-Annealing-Systeme mit über 5000
Qubits, die für Optimierungsprobleme geeignet sind.
Rigetti Computing (USA):
Standort:
Berkeley, Kalifornien (USA).
Quantencomputer:
Entwickeln supraleitende Quantencomputer mit zunehmender Qubit-Zahl
und Integration in Cloud-Dienste.
Zukunftsaussichten
Skalierung
und Stabilität:
Die wichtigsten Herausforderungen bleiben die Skalierung der
Qubit-Anzahl und die Verbesserung der Fehlerkorrektur.
Fortschritte
in diesen Bereichen werden entscheidend dafür sein, wann und wie
Quantencomputer praktisch nutzbar werden.
Verbreitung:
Obwohl große Quantencomputer derzeit hauptsächlich in
Forschungszentren und bei großen Unternehmen betrieben werden, wird
erwartet, dass der Zugang zu Quantencomputing-Diensten über
Cloud-Plattformen weiter zunimmt, wodurch auch kleinere Unternehmen
und Forschungseinrichtungen Zugang zu dieser Technologie erhalten.
Private
Nutzung:
Ein privater
Besitz von Quantencomputern für den Heimgebrauch ist derzeit
unrealistisch
und bleibt wohl auch in den nächsten Jahrzehnten unwahrscheinlich,
da die Technologie weiterhin hochkomplex und kostenintensiv ist.
Quantencomputing ist ein dynamisches und
schnell wachsendes Feld, das weiterhin weltweit erhebliche
Investitionen und Innovationen erfährt.
Es bleibt spannend zu
beobachten, wie sich diese Technologien weiterentwickeln und welche
Durchbrüche in den kommenden Jahren erzielt werden.
-----------------------------------------------------------------------------------------------------------------------------------------------------
Für Interessierte: Mathematische
Hintergründe
Ich habe bewusst die mathematischen
Grundlagen und Beschreibungen nach hinten geschoben, denn man sollte
zunächst die größeren Zusammenhänge erfassen. Mathematische
Darstellungen sind für viele abschreckend, da die Formelsprache und
die Darstellungen nicht jedem geläufig ist und daher für das
Verständnis eher behindernd als förderlich ist. Da man jedoch in
vielen Publikationen und Zusammenfassungen auf mathematische
Beschreibungen und Darstellungen stößt, versuche ich nachfolgend,
einen möglichst einfachen Zugang zu dieser Formelsprache zu
schaffen.
Bevor wir zur
Bloch-Kugel kommen, lass uns kurz wiederholen, was ein Qubit ist:
Qubit
steht für Quantenbit.
Es ist die kleinste Informationseinheit in einem Quantencomputer,
ähnlich wie ein Bit
in einem klassischen Computer.
Ein
Bit
kann nur entweder den Wert 0
oder 1
darstellen.
Ein Qubit
kann gleichzeitig
in den Zuständen 0
und 1
sein. Das nennt man Superposition.
Die Ket-Notation
Diese ist eine Art, die Zustände eines Qubits
mathematisch aufzuschreiben. Das "Ket"-Symbol zeigt an,
dass wir einen Quantenzustand messen:
|>
heißt „Ket“ und wird verwendet, um Quantenzustände
zu kennzeichnen.
|0>
bedeutet, dass das Qubit im Zustand 0
ist.
|1>
bedeutet, dass das Qubit im Zustand 1
ist.
Sie ist ein Modell, um den Zustand eines
Qubits bildlich darzustellen. Stell dir eine Kugel
vor, ähnlich wie einen Globus:
Nordpol
der Kugel:
Repräsentiert den Zustand |0>
(sprich: „Ket Null“)
Südpol
der Kugel:
Repräsentiert den Zustand |1>
(sprich: „Ket Eins“)
Oberfläche
der Kugel:
Jeder Punkt steht für einen möglichen Zustand des Qubits,
inklusive aller Superpositionen zwischen |0>
und |1>.
50% wären dann am Äquator der Kugel.
Wie wird ein Qubit mathematisch
beschrieben?
Ein Qubit kann gleichzeitig
im Zustand |0> und |1> sein.
Das schreiben wir so:
|ψ>
= α * |0>
+ β * |1>
Hier bedeuten die Symbole:
„Ket
Psi“ ist
der Gesamtzustand des Qubits.
alpha
und beta
sind Zahlen, die angeben, wie viel von |0>
und |1>
im Quantenzustand enthalten ist.
alpha und beta sind in den oben beschriebenen
Fällen gleich. Die Wahrscheinlichkeit ist jeweils 50%.
Wichtig: Die Summe
der Quadrate absoluten Beträge dieser Zahlen muss 1
(also 100%) ergeben.
Die jeweiligen Quadrate entsprechen der
Wahrscheinlichkeit, diesen Zustand zu messen.
alpha und beta
wären hier 0,7071 (Kehrwert der Wurzel von 2), denn das Quadrat
ergibt 1/2 oder 0,5, was 50% entspricht.
|α|²
+
|β|² =
1
Das bedeutet, wenn wir
den Zustand messen, bekommen wir mit 50 %
Wahrscheinlichkeit |0>
und mit 50 %
Wahrscheinlichkeit |1>.
Ein
Messvorgang hebt die Superposition sofort auf.
Zusammenfassung:
Das
"Ket"-Symbol zeigt den Quantenzustand an.
Ket Psi ist
der Gesamtzustand des Qubits in seiner Superposition.
Ket 0 und
Ket 1 sind die beiden Basiszustände eines Qubits.
alpha und
beta sind Zahlen, die den Anteil der beiden Basiszustände im
Gesamtzustand anzeigen.
Die Quadrate der absoluten Beträge von
alpha und beta stehen für die Wahrscheinlichkeit, diese
Basiszustände zu messen.
Was
ist die Hadamard-Matrix?
Die Hadamard-Matrix ist eine
fundamentale Matrix in der Quanteninformatik und repräsentiert das
Hadamard-Gatter, ein Quantenlogikgatter.
Dieses
Gatter wird verwendet, um ein Qubit in eine Superposition
zu versetzen, also in einen Zustand, in dem es gleichzeitig |0>
und |1> ist.
Mathematische
Darstellung der Hadamard-Matrix
Die
Hadamard-Matrix H
ist eine 2×2-Matrix
und wird wie folgt geschrieben:
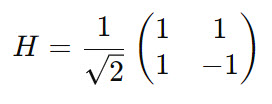
H bezeichnet die Hadamard-Matrix. Der Kehrwert
der Wurzel von 2 ist ein Skalierungsfaktor, der sicherstellt, dass
die Gesamtwahrscheinlichkeit nach der Anwendung des Gatters erhalten
bleibt.
Die Matrix selbst verfügt über 2 * 2 = 4 Elemente. Die
Matrix hat zwei Zeilen und zwei Spalten. Die Zahlen in der Matrix
bestimmen, wie die Eingabewerte transformiert werden.
Ein
Qubit kann in den Zuständen |0>
oder |1> sein oder in einer Superposition dieser
Zustände. Diese Zustände können als Vektoren dargestellt
werden:

Wie wirkt nun das Hadamard-Gatter?
1.
Auf den Zustand |0>

1.
Auf den Zustand |1>

In beiden Fällen, also auch im Falle
des negativen Vorzeichens, ergibt sich durch das Quadrat des
absoluten Betrages von alpha und beta jeweils 1/2 oder 0,5
oder 50%.
Technisch ist wichtig,
dass man weiß, wie man eine Matrix mit einem Vektor
multipliziert:
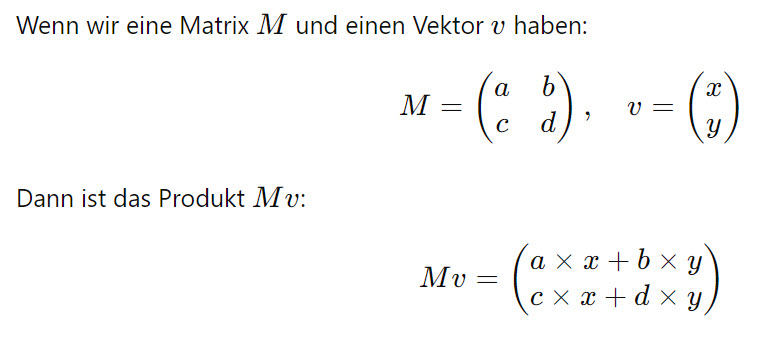
Man kann sich merken, dass das Hadamard-Gatter
den Zustand eines Qubits auf der Bloch-Kugel um eine
bestimmte Achse dreht, sodass es von einem Pol (eindeutiger Zustand)
zum Äquator (Superposition) bewegt wird. Der Äquator entspricht
hier einem Quantenzustand der Überlagerung der beiden Pole mit einer
50% Wahrscheinlichkeit der Messung für beide Pole.
Nun schauen wir uns noch das CNOT-Gatter
an, da hier zwei Qubits verschränkt werden.
Das CNOT-Gatter (Controlled
NOT-Gatter) ist ein fundamentales Quantenlogikgatter, das mit zwei
Qubits arbeitet:
Kontroll-Qubit:
Dieses Qubit bestimmt, ob eine Aktion ausgeführt wird.
Ziel-Qubit:
Dieses Qubit wird verändert, abhängig vom Zustand des
Kontroll-Qubits.
Das CNOT-Gatter folgt einer einfachen Regel:
Das CNOT-Gatter wird genutzt, um zwei
Qubits zu verschränken. Dies bedeutet, dass der Zustand des
einen Qubits untrennbar mit dem Zustand des anderen Qubits verbunden
ist.
Das Kontroll-Qubit wird mit dem Hadamard-Gatter in
folgenden Zustand der Superposition versetzt:
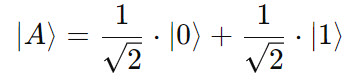
Das Ziel-Qubit befindet sich im
Anfangsquantenzustand |0>.
Das CNOT-Gatter wird nun auf Qubit
A (Kontroll-Qubit) und Qubit B (Ziel-Qubit)
angewendet.
Aufgrund der Superposition von Qubit A wirkt das
Gatter auf beide Bestandteile der Superposition.
Nach der
Anwendung des CNOT-Gatters ist der gemeinsame Zustand der beiden
Qubits:
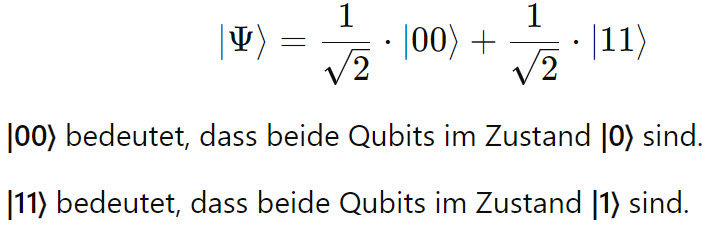
Matrixdarstellung des CNOT-Gatters
Das CNOT-Gatter kann mathematisch durch eine
4×4-Matrix dargestellt werden, da es auf zwei
Qubits wirkt und jedes Qubit zwei mögliche Zustände hat.
Anordnung der Zustände
Wir ordnen die vier möglichen Zustände der
zwei Qubits wie folgt:
|00>
|01>
|10>
|11>
CNOT-Matrix
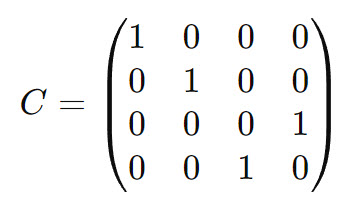
Erklärung der Matrixelemente
Wie wirkt die Matrix auf die
Zustände?
Eingangszustand
|00>:
Eingangszustand
|01>:
Eingangszustand
|10>:
Eingangszustand
|11>:
Schaltbild des CNOT-Gatters
Das CNOT-Gatter wird in Quanten-Schaltkreisen
durch folgende Symbole dargestellt:

Erklärung der Symbole
(Punkt):
Repräsentiert das Kontroll-Qubit.
(Kreis
mit Kreuz):
Repräsentiert das Ziel-Qubit,
auf das die NOT-Operation
angewendet wird.
Vertikale
Linie:
Verbindet das Kontroll-Qubit mit dem Ziel-Qubit und zeigt die
Abhängigkeit der Operation an.
Zusammenfassung
CNOT-Gatter:
Ein
fundamentales Quantenlogikgatter, das zwei Qubits miteinander
verschränkt.
Ändert
den Zustand des Ziel-Qubits basierend auf dem Zustand des
Kontroll-Qubits.
Verschränkung:
Matrixdarstellung:
Schaltbild: